 去年在知道表弟要考會考時,我順便研究了一下網路上有哪些可以使用的會考自學輔助教材,以下也推薦給大家~1.國中會考歷屆試題網站
去年在知道表弟要考會考時,我順便研究了一下網路上有哪些可以使用的會考自學輔助教材,以下也推薦給大家~1.國中會考歷屆試題網站410211 發表在 痞客邦 留言(0) 人氣(991)
410211 發表在 痞客邦 留言(0) 人氣(974)
410211 發表在 痞客邦 留言(0) 人氣(272)
410211 發表在 痞客邦 留言(0) 人氣(166)
410211 發表在 痞客邦 留言(0) 人氣(124)
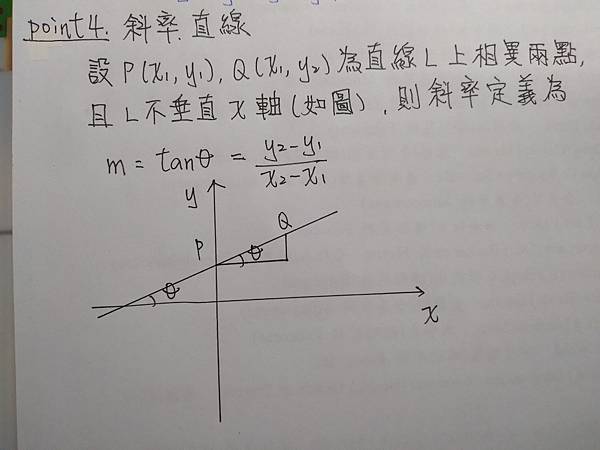 在平面上為了描述一條直線傾斜的情形,或者界定直線的方向,我們定義直線和直角座標系 x 軸所夾之最小正角 θ 為斜角。
在平面上為了描述一條直線傾斜的情形,或者界定直線的方向,我們定義直線和直角座標系 x 軸所夾之最小正角 θ 為斜角。 410211 發表在 痞客邦 留言(1) 人氣(34,378)
410211 發表在 痞客邦 留言(0) 人氣(1,024)
 一、一元一次方程式二、一元二次方程式
一、一元一次方程式二、一元二次方程式410211 發表在 痞客邦 留言(0) 人氣(143)



